To read about this tuning in its right place, click HERE
And in the video you can hear a version of my tuning with 36 tones pr. octave :
IN TUNINGLAND
After
a lot of work with my website
TU
you – a change to TU and
living with the imperfections of these tunings, it became
natural for me to move on working with tunings with more than 12
pitches per octave. "In Tuningland" is a result of these
efforts.
In
Tuningland (IT) is a new idea (presumably) to tune and
arrange ordinary keyboards etc. IT operates in the fields of
"Just Intonation" with pure or almost pure chords and
hides the problem of the comma to quite a large extent.
And
my main goal has been that IT can be useful in some way on acoustic
instruments.
Along
the way in this work, my assessment of the application has shifted
between consider IT as just a funny curiosity, and towards that IT
can actually have a musical significance.
The
last part of this long process resulted in recordings with 2
acoustic harpsichords and two musicians.
After
this last experiment IT is now upgraded and confirmed in my mind to
at least "social and musical fun in the rehearsal room" !
Since
it is easier to play this tuning with 2 or more musicians, let me
therefore call it a social tuning. :)
After
the acoustic tests and recordings, I also found that I would give
harpsichord players an opportunity to test this without having to go
too much into the theory.
So
this shortcut is for you: first an untempered (not my favorite)
version of IT with easy tunings instructions and audio files from
real harpsichords.
In the bottom of the page you will see a link to tuning instructions for In Tuningland in tempered versions.
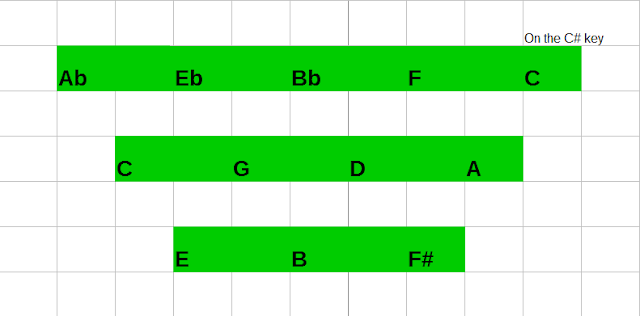
If you've ever longed to play pure chords on your harpsichord , you'll get exclusively pure chords from Ab inclusive E (seen from the circle of fifths).
In the bottom of the page you will see a link to tuning instructions for In Tuningland in tempered versions.
If you've ever longed to play pure chords on your harpsichord , you'll get exclusively pure chords from Ab inclusive E (seen from the circle of fifths).
Click
HERE
Another acoustic instrument I've had in mind is the accordion.
This
instrument is like the harpsichord rich in overtones and the
difference between tunings becomes significant. Unfortunately,
the accordion is not as easy to tune as a harpsichord.....
If you will anticipate hearing my digital recordings
you can find them by scrolling down HERE.
And finally a piece for digital church organ with comparings between 3 variants of In Tuningland + 1/4 and 1/6 comma meantone and 12-ET (Equal temperament)
Click HERE !
If you experience alternative tunings strange, it might be a blend of the fact that 12-ET is ubiquitous in our world and therefore feels unaccustomed, together with the syntonic comma as a problem that still can be present in different subtle ways when working with pure intervals.
I will recommend this introduction to "In Tuningland" also to those who are more interested in the problem of the syntonic comma than in this spesific tuning. This comma is present in all traditional Western music, and not only for the keyboard players. This website has a lot of audio files combined with understandable lattices that provide insight into these issues.
These
terms will be explained, visualized and "audiolized"
:
1.
Comma shift
2.
Comma drift
3.
Wolf intervals
These
phenomena are problems but actually also solutions.
In addition, there are many comparisions with traditional temperaments (Meantones (1/4&1/6,Equal T.) where you can judge by yourself and train your ear at the same time.
For those familiar with the terminology you can click below on the table of contents for a quick survey :
1. Arranging of the keyboard
2. Supplementary and overlapping setup
3. Halving the comma shift
4. Economizing amount of pitches
5. Small adjustments (tempering)
6. Expansions
7. Comprehensive setups
And here are the pluses and minuses with IT (click)
......................................................................................................................
In this guide to "In Tuningland", I will like to use completely pure intervals and chords.
Then
what is right and what is wrong will be very clear.
Due to an extensive use of audio files combined with lattices, I can postpone the use of cent values and the
calculation until the end of this introduction.
The
fascination of tuning and the frustration that the world of fifths
and world of thirds doesn`t fit together have haunted musicians for
centuries. Common to all endeavors lies in dealing with commas, not
least the syntonic comma.
The
syntonic comma is the most important comma, in any case
in traditional western music.
This
comma is markedly present when string players intonate. (The
Pythagorean comma, which is maybe more often mentioned, refers to
tuning of keyboard instruments and to solo instruments more indirectly)
The
fact is: if we tune 4 pure fifths one after another, such as
Bb-F-C-G-D, then this D, named by me as "D 0", is annoying higher than the
one we get when tuning a pure major third from the same starting
point, Bb-D (named "D -2").
The difference between "D 0" and "D-2" is exactly one syntonic comma (in this untempered version)
The difference between "D 0" and "D-2" is exactly one syntonic comma (in this untempered version)
The
reason why I define the difference as two units (D 0 and D -2) is that I
will be completely consistent in my explanations to avoid confusions.
Later we want to use 1 unit , a half of a comma.
1. Arranging of the keyboard
1. Arranging of the keyboard
My
starting point is pure thirds and fifths on a regular keyboard in C
major.
This C-setup is marked C
This C-setup is marked C
In C, pure
C major, F major, Dm, Am, Em, G major, Bb major, D major, A major, E major
are prioritized.
For
this we need 2 D`s, where the highest is placed on the Eb key !
Before
this is getting too confusing, we will hurry to our first listening
example.
Such
a tuning contains many chords, but because of the problem with the
comma, it also has big limitations, so it is not usable for so much
music.
I
will nevertheless demonstrate all the 3-tone major and minor triads in a small piece where I've steered away from the comma
problem, but the curse of the comma will appear in the end. : (
......................
Video (music piece) : C 0 Passing through all pure 3-tones triads + many more
..............................
..............................
Important:
The
observant listener will see and hear that:
Pure
major thirds are obtained from
the fifth row below (- 2 units).
Pure
minor thirds are obtained from the fifth row above(+ 2 units)..
..........
A
pure sus4 chord is 3 tones (2 fifths) horizontally in a row.
Furthermore,
we see that a pure D sus4 in this first example, C, is missing (No
G-D-A in a horizontal line).
Around
G-D-A there are major problems, we have a pure G-(high)D and a pure (low)D-A ,
but with 2 different D`s, not successive.
Pure intervals will easily make some other wolf intervals.
The intervals between the red tones below are wolfs, they are not neighbors on a row in the diagram.
But if we avoid them we have actually 3 similar diatonic scales
First C major
C-D(on Eb key)- E- F- G- A-B- C
If we only use one of the red tones at a time (avoid the wolf fifth (high)D-A) , we will get a very pure feeling with cluster possibilities.
The tritonus is as pure as possible.
Notice that the minor third D-F is not pure , but can be used.
Then we have F major.
F-G-A-Bb-C-D(the lower one)E-F
Only use one red tone at a time (avoid the wolf G-(low)D). G-Bb is not pure.
The nice thing is that on the other side of the Dsus4 division (from the view of circle of fifths) we will find exactly the same possibilities in A major (do not play B and F# at the same time).
Only use one red tone at a time.
A-B-C#-D(the lower one)-E-F#-G#-A
Pure intervals will easily make some other wolf intervals.
The intervals between the red tones below are wolfs, they are not neighbors on a row in the diagram.
But if we avoid them we have actually 3 similar diatonic scales
First C major
C-D(on Eb key)- E- F- G- A-B- C
If we only use one of the red tones at a time (avoid the wolf fifth (high)D-A) , we will get a very pure feeling with cluster possibilities.
The tritonus is as pure as possible.
Notice that the minor third D-F is not pure , but can be used.
Then we have F major.
F-G-A-Bb-C-D(the lower one)E-F
Only use one red tone at a time (avoid the wolf G-(low)D). G-Bb is not pure.
The nice thing is that on the other side of the Dsus4 division (from the view of circle of fifths) we will find exactly the same possibilities in A major (do not play B and F# at the same time).
Only use one red tone at a time.
A-B-C#-D(the lower one)-E-F#-G#-A
To be familiar with this setup in C, it is very useful to play these scales and chords.
Also highly recommended is to play 2 melodic minor scales with their associated chords.
First in A minor.
Don`t use B and F# at the same time Avoid ii -chord
A-B-C-D-E-F#-G#-A
So D minor, avoid G-D at the same time .
Avoid IV -chord
Here we can play I-ii-V-I (D(m)-Em-A-D(m))
D-E-F-G-A-B-C#-D
If you have tried scales and chords in this setup, you are ready for a transposing to Bb
............................................
2. Supplementary and overlapping setup
Also highly recommended is to play 2 melodic minor scales with their associated chords.
First in A minor.
Don`t use B and F# at the same time Avoid ii -chord
A-B-C-D-E-F#-G#-A
So D minor, avoid G-D at the same time .
Avoid IV -chord
Here we can play I-ii-V-I (D(m)-Em-A-D(m))
D-E-F-G-A-B-C#-D
If you have tried scales and chords in this setup, you are ready for a transposing to Bb
............................................
2. Supplementary and overlapping setup
If
we transpose this tuning to Bb we get 2 C`s (instead of 2 D`s), the
highest of them is placed on the C# key. .
Now
we see that we have both a pure Dsus4 (G-D-A) and the opportunity to
play a pure Dm-G (not 7th) -C progression. The problem has been moved to Csus4.
F-C-G
The text about scales and chords from C 0 above , are transposed to Bb HERE !
The text about scales and chords from C 0 above , are transposed to Bb HERE !
But couldn`t
we just let Bb take
over when we meet problems in C ??
Here I have merged them with a common area in grey.
Here I have merged them with a common area in grey.
Like
this:
But
then we get a new big problem. We end up somewhere else than
where we started, a phenomenon called comma drift.
Hear and see this in extreme, only pure chords, and the common tones between the chords are the same.
This is the syntonic comma at its worst and funniest :)
Video: RISING !
Video: FALLING !
Hear and see this in extreme, only pure chords, and the common tones between the chords are the same.
This is the syntonic comma at its worst and funniest :)
Video: RISING !
Video: FALLING !
Bb,
is resolving something by giving other chords and scales, but we still have the urgent comma problem.
.....................................
3. Halving the comma shift
3. Halving the comma shift
Here
we are in the core of "In Tuningland".
We
now raise Bb by
half of a comma, to a Bb +1.
Like this :
Then we will get a D in Bb +1, now denoted as D -1 that will end in the middle of D 0 and D-2 in C 0.
Like this :
The same displayed in another way :
Then we will get a D in Bb +1, now denoted as D -1 that will end in the middle of D 0 and D-2 in C 0.
The comma shift is halved while these two manuals complement each
other chordally.
And
if we go to the problem with the two C's in Bb
+ 1 which after the rising gives them the names C +1
and C -1,then we see that C 0 from C
0 is lying in the middle of these two tones in the same way.
If
we are to sum up this IT variant with the lowest amount of pitches (24),
which can be tuned on a two-manual harpsichord, then we now can see that
these manuals are overlapping and complementing each other in a nice way.
1.
Some chords are only available just on one manual.
Some
chords are to be found on both manuals.
2.
Some chords are pure just on one manual.
Some
chords are pure on both manuals.
3.
You can change the manual when the curse of the comma threatens.
In
a way, we have a comma shift and a comma drift at the same time, but only the half of it.
Now
we have complementary setups with a halved comma shift.
A
nice thing : We have Dm, Am, Em,......, F#m , C#m , but miss Bm in C 0
But
we do have Bm in Bb+1 (which is a more distant key) !
In the two first examples I am dancing with the wolfes :) :
C 0 with the comma problem : Video HERE
Bb+1 with the comma problem : Video HERE
.................................................................
C0 and Bb+1 combined, and the comma problem reduced: Video:HERE
A survey for the chords is available HERE.
4. Economizing amount of pitches
But it is much more difficult to find a tuning that is economizing regarding amount of pitches and opens up for using it in a acoustic way.
In the two first examples I am dancing with the wolfes :) :
C 0 with the comma problem : Video HERE
Bb+1 with the comma problem : Video HERE
.................................................................
C0 and Bb+1 combined, and the comma problem reduced: Video:HERE
The
chords from C 0 and Bb
+1 are interlaced into each other.
Some
chords have a bit higher pitch in Bb +1 than
in C 0 and
vice verca.
A survey for the chords is available HERE.
I
started with C 0 because
it is easiest to understand and I have taken a starting point in
this. However, if we look at the range in scales and chords, it is
maybe more natural selecting F
0 and G-1 to
get C major as the center.
Here
is a view of the scales (not chords):
| Bb +1 C 0 | F 0 G -1 |
| Eb major | Bb major |
| Bb major | F major |
| F major | C major |
| C major | G major |
| G major | D major |
| A major | E major |
| C minor | G minor |
| G minor | D minor |
| D minor | A minor |
| A minor | E minor |
4. Economizing amount of pitches
This
is an economizing model and can not be compared with the digital
world's approach to infinite pitch adjustments.
Working
with Just Intonation on digital instruments:
you
can take a look on this APP,
and
this SOFTWARE.
But it is much more difficult to find a tuning that is economizing regarding amount of pitches and opens up for using it in a acoustic way.
Because
of the relative few pitches IT can be used on one or several double
manual harpsichords. Just Intonation is really something different
playing it acoustically.
"Yes, many find the purity of computer-generated sounds utterly unnatural. The reason is that there will be a fixed pattern of phase cancellation among some of the coinciding partials depending on your onset times. This frozen pattern of phase cancellation does not occur in real music, where phase relationships among coinciding partials will cycle between constructive and destructive. Without this effect, the dyad or chord will sound like a single timbre rather than a harmony." Paul Erlich
Of course you can (like me) use In Tuningland in a digital way, if your keyboard/software allows IT.
5. Small adjustments (tempering)
Until now we have operated exclusively with pure intervals.
Those who will try to tune their double-manual harpsichord can use this table. Or you can tune by ear using TUNING INSTRUCTIONS
You can do it on a digital keyboard too, but if the two pitches of D in C 0 and two Cs in Bb+1 make troubles then it will be better using the spreadsheets. Explanation below.
Those who will try to tune their double-manual harpsichord can use this table. Or you can tune by ear using TUNING INSTRUCTIONS
You can do it on a digital keyboard too, but if the two pitches of D in C 0 and two Cs in Bb+1 make troubles then it will be better using the spreadsheets. Explanation below.
If the comma shift still is annoying then my solution and maybe my favourite version is to narrow/temper all fifths with 1 cent. Then the comma shift will decrease from 10,8 to 8,8 cent.
Here is the table for this.
Here is the table for this.
You can use the
spreadsheet to find your own solution. See further down.
The tempered version is used both in
15 HYMNS,
the acoustic harpsichord recordings and
2 simple improvisations.
My (digital) accordion recordings with comparing possibilities
can be heard HERE. (Read or scroll down)
There are pluses and minuses when chosing the quality of the fifths.
Take a look : HERE
The tempered version is used both in
15 HYMNS,
the acoustic harpsichord recordings and
2 simple improvisations.
My (digital) accordion recordings with comparing possibilities
can be heard HERE. (Read or scroll down)
There are pluses and minuses when chosing the quality of the fifths.
Take a look : HERE
Here is a collection to get familiar with In Tuningland in the smallest version (24 pitches). It is 15 hymns with lattices and I have also lowered the speed. In slow tempo you get an opportunity to follow the idea and is my best examples to explain the idea.
You can also choose to compare IT with 1/4 comma meantone and Equal temperament.
VIDEOS, 15 Hymns : HERE
6. Expansions
The principle of "In Tuningland" can be expanded.
By
replacing only 5 tones in C
0 we get exactly the corresponding setup transposed
to Ab,
marked
as Ab +2.
In the same way as in C 0 and Bb +1 we have two pitches of a tone, in Ab +2 we have Bb:
Bb 0 and a Bb +2, the latter on the B key.
In the same way as in C 0 and Bb +1 we have two pitches of a tone, in Ab +2 we have Bb:
Bb 0 and a Bb +2, the latter on the B key.
And
if we replace 5 tones in Bb
+ 1 we can get D
-1.
Here we have two pitches of E :
E-3 and E-1, the last placed on the F key.
Here we have two pitches of E :
E-3 and E-1, the last placed on the F key.
Tables
of the chords available , where to find and which is highest in
pitch: HERE
Below you will find the notes interlaced.
The darkest red is common for Ab+2 and C 0
The darkest green is common for Bb+1 and D-1.
The five tones in lilac on the top belongs to Ab+2.
The five light red to the right belongs to C 0.
The five lighter green notes in 2nd row belongs to Bb+1.
The five light green notes to the right belongs to D-1.
IT provides here a wide range of chords using 34 pitches.
In this piece I will show some of the possibillities. Everytime I shift keyboard/setup there will come a sign up to the left.
And you can compare it with common temperaments.
In meantone (1/4&1/6) only 8 major thirds are useful.
In my comparisions I use extended meantone, that means
more than 12 pitches pr.octave, similar to keyboards with split keys . Here my focus is on the qualtites of the sound and not the practical solutions for the meantones.
Here it must be admitted that when we use the version of -1 cent tempered fifths, my favorite, and the sound has a little less treble and it is a bit fuller, so the difference to the meantone(1/4) is not so great as expected. But you can hear it.
Here is the right time for you to judge by yourself and train your ears using my little organ piece
"A PURE MIX"
..............................
Of course, economic use of the number of pitches is not so important in the advanced part of the digital tuning world, and even with two acoustic harpsichords we are still using 48 keys on these 34 pitches.
But used on an archicembalo this will be of utmost importance.
(See spreadsheet link to archicembalo down below.)
It would be nice to test In Tuningland on a harpsichord or organ
with Vicentino`s keyboard idea !
https://en.wikipedia.org/wiki/Archicembalo
And if IT is used on an organ (like the Groven organ) where the right pitch is chosen automatic, the advantage of few pitches is obvious.
7. Comprehensive setups
In the beginning of this introduction I was promoting a nice version for 2 harpsichords .
HERE you can check how many tones that is common in a couple of setups with same color.
......................................................................................................
Then
to the :
SPREADSHEETS
They are made in LibreOffice (It is free to download)
But you can open them in Excel too.
Below you will find the notes interlaced.
The darkest red is common for Ab+2 and C 0
The darkest green is common for Bb+1 and D-1.
The five tones in lilac on the top belongs to Ab+2.
The five light red to the right belongs to C 0.
The five lighter green notes in 2nd row belongs to Bb+1.
The five light green notes to the right belongs to D-1.
IT provides here a wide range of chords using 34 pitches.
In this piece I will show some of the possibillities. Everytime I shift keyboard/setup there will come a sign up to the left.
And you can compare it with common temperaments.
In meantone (1/4&1/6) only 8 major thirds are useful.
In my comparisions I use extended meantone, that means
more than 12 pitches pr.octave, similar to keyboards with split keys . Here my focus is on the qualtites of the sound and not the practical solutions for the meantones.
Full tempo |
1/2 tempo |
1/3 tempo |
|
IT Pure fifths |
VIDEO |
VIDEO |
VIDEO |
IT -1 cent fifths |
VIDEO |
VIDEO |
|
IT -2 cent fifths |
VIDEO |
VIDEO |
|
1/4 c meantone |
VIDEO |
VIDEO |
|
1/6 c meantone |
VIDEO |
VIDEO |
|
Equal temperament |
VIDEO |
VIDEO |
Here it must be admitted that when we use the version of -1 cent tempered fifths, my favorite, and the sound has a little less treble and it is a bit fuller, so the difference to the meantone(1/4) is not so great as expected. But you can hear it.
Here is the right time for you to judge by yourself and train your ears using my little organ piece
"A PURE MIX"
..............................
Of course, economic use of the number of pitches is not so important in the advanced part of the digital tuning world, and even with two acoustic harpsichords we are still using 48 keys on these 34 pitches.
But used on an archicembalo this will be of utmost importance.
(See spreadsheet link to archicembalo down below.)
It would be nice to test In Tuningland on a harpsichord or organ
with Vicentino`s keyboard idea !
https://en.wikipedia.org/wiki/Archicembalo
And if IT is used on an organ (like the Groven organ) where the right pitch is chosen automatic, the advantage of few pitches is obvious.
7. Comprehensive setups
Under
point 6. the number of chords was expanded using 4 setups: Ab
+2, Bb +1, C
0 and D -1.
Apart
from the very nice growth of chords, flexibility does not get so much
better.
In the beginning of this introduction I was promoting a nice version for 2 harpsichords .
We
can use Bb +1, F
0, C 0 and G
-1 (32 pitches per octave).
This
system provides much better handling of passing tones and will allow
access to some material from the renaissance. The advantage of 2
cembalists is that each of them has only 2 tones on the wrong keys
each to keep track of. And with 2 players we will get much more
smooth transitions regarding switching of the manuals. See the
acoustic and practical page to this idea. HERE
!
HERE you can check how many tones that is common in a couple of setups with same color.
This
combination provides 2 additional major triads compared to meantone.
We
can play pure Ab, B and G#m. Actually we can also play a pure Fm with
a combination of 2 manuals (F-C on G-1 and
Ab on Bb +1)
Tables of the chords available , where to find and which is highest in pitch:
Tables of the chords available , where to find and which is highest in pitch:
The
dark red is common for C
0 and F 0,
The
dark green is common to Bb
+1 and G -1
The
lilac to the right is only for C
0,
The
lilac to the left only for F
0
The
light green on the top is only for Bb
+1,
The
yellowish green to the left is only for for G
-1.
......................................................................................................
SPREADSHEETS
They are made in LibreOffice (It is free to download)
But you can open them in Excel too.
The simplest spreadsheet: C 0 and Bb +1 (Click and download)
Under the green INPUTs you will find the cells where you can enter a variable.
The green INPUT at the top to the right is just a calculator where you can have comma shift as a variable.
The calculator has no effect on the main tables.
Up to the left you will find:
I always let the major third be pure (0) , but if you want another value you can change it.
The cell for the fifths is important. If you enter -1 (my favourite) in the Fifth cell, you will see a double reduction (-2 cent) of the comma shift from 10,753 to 8,753.
Then you have 3 INPUTs to the left around C0
If the yellow and blue cells are set to 0 and you enter the values for a setup into a synthesizer or a tuning app, than the tones with a square will be a semitone too high.
Therefore set the blue cell to - 100 to lower these tones with a semitone.
But then these values will get a very low value.
Many synthesizers don`t allow values outside -63/+63.
To fix that enter a positive value into the yellow cell
eg +50. Then all the values will come inside this range.
Another BUT:
But then the cent values will be too high and your desired concert pitch (eg 440 Hz) will be far from right.
So therefore enter eg 440 into the brown cell and just to the right in the light brown cell you will get a Hz value to enter to get the right pitch.
Now everything is fine and you can enter cent numbers for the different setups, in our example C0 with one extra D, and Bb+1 with one extra C, both in squares.
....................................
If you want to delete a setup from the selection in a spreadsheet, then highlight the rows in the margin to the left.
A right click, and delete !

Therefore set the blue cell to - 100 to lower these tones with a semitone.
But then these values will get a very low value.
Many synthesizers don`t allow values outside -63/+63.
To fix that enter a positive value into the yellow cell
eg +50. Then all the values will come inside this range.
Another BUT:
But then the cent values will be too high and your desired concert pitch (eg 440 Hz) will be far from right.
So therefore enter eg 440 into the brown cell and just to the right in the light brown cell you will get a Hz value to enter to get the right pitch.
Now everything is fine and you can enter cent numbers for the different setups, in our example C0 with one extra D, and Bb+1 with one extra C, both in squares.
....................................
If you want to delete a setup from the selection in a spreadsheet, then highlight the rows in the margin to the left.
A right click, and delete !

You will find the spreadsheets here with several combinations of the setups.
------------------------------------------------
I hope you will like "In Tuningland" , whether it is from
a musical, educational or meditative point of view .
Gunnar Tungland, september 2017













Ingen kommentarer:
Legg inn en kommentar